How to Solve Questions based on Simple & Compound Interest?

Simple Interest

Simple interest is defined as the principal amount of a loan or deposit made into a bank account. The total dollar amount of interest is determined by how long it takes to repay the loan.

Simple interest is calculated using the following formula:

Simple Interest=𝑃×𝑟×𝑛

where: 𝑃=Principal amount

=Annual interest rate 𝑛

=Term of loan, in years​

Compound Interest

Compound interest is more complex. Unlike simple interest, compound interest accumulates or grows over time. You earn interest on both the principal and any past interest payments. If you borrow money with compound interest, you will pay interest on both the principal and any interest that has accrued. If you deposit money in a bank, the interest payment on your money will increase over time in real currency terms.

Interest can be compounded daily, monthly, quarterly, semi-annually, or annually. The frequency at which it is compounded determines how much you earn or pay.

The formula for compound interest is:

Compound Interest=𝑃×(1+𝑟)𝑡−𝑃

where: 𝑃=Principal amount 𝑟

=Annual interest rate 𝑡

=Number of years interest is applied

What is the major difference between Simple and Compound Interest ?

Simple interest is calculated on the main amount or loan amount, whereas compound interest is calculated on both the principal amount and the interest accumulated during a specific time or prior period.

Solved Examples:

Q.1. Amrit borrowed Rs. 40,000 for 2 years at the rate of 6% per annum. Find the simple interest.

Solution.

Give, P= Rs. 40,000; R= 6%; T= 2 Years

SI= P*R*T/100

SI= 40,000*6*2/100 = Rs. 4800

Q.2. A sum of Rs. 50,000 was deposited for 3 years at 105 per annum, compounded annually. The difference between the interest for 2 years and that for 3 years is:

Solution.

Given, Principal= Rs. 5,000.

Time= 3 years

Rate= 10%

Formula used: Amount = A = P x (1+) nt
Where,
P = Principal
R Rate of interest
T = time in years C.I. (Amount – Principal)
Where, C.I. Compound Interest.
CALCULATION:
Here, P= 5,000, T=3, R=10%
Amount for 3 years – AS-Px(1+r/100)t
5000×(1+10/100)3
A3-5000 × 11/10×11/10 × 11/10 -6,655.
Now, C.I. for 3 years. Amount – Principal 6655-5000 Rs 1655.
Amount for 2 years = A2 = 5000 ×(1+ 10/100)2
5000 × 11/10 × 11/10 -6,050.
C.I. for 2 years (Amount-Principal)
6050-5000 Rs1050.
Now, Difference (C.I. for 3 years – C.I. for 2 years) (1655-1050) – Rs. 605

Q.3. A person deposited a sum of Rs. 5000 in a bank at 5% per annum simple interest. Another person deposited Rs. 5000 at 8% per annum compound interest. After two years the difference of their interest will be?

Solution

C.I. for 1 person= 5000*2*5/100 = Rs. 500

C.I. for 2nd person = 5000* [ (1+ 8/100)²   – 1]

5000* [ (1+ 8/100)²   – 1]

= 5000 [ (27/25)²– 1]

= 5000 [ 729-625/625]

= 5000*104/625

= Rs.832

Thus, Difference in interest= Rs. 832- Rs. 500= Rs. 332

Q.4. The ratio of CI for 3 years and SI for one year for a fixed amount at a rate of r% is 3.64. What is the value of r (approx.)?

Solution

Given, CI for 3 years: SI for 1 year= 3.64

Concept: Here in this question the most important thing is that approximate value is to be calculated when the ratios is given between compound interest and simple interest.

Formula used: ([1 + (r/100)² ]-1)/(r/100)=3.64

Calculation:

1+ (r/100)² = 1 + (3.64r/100)

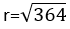
r= 20%

Q.5. A sum was borrowed at 20% p.a. compound interest. It was repaid in 3 annual installments with each installment being paid at the end of a year. The first, second and third installments were Rs.1200, Rs.1152 and Rs.2592 respectively. Determine the sum borrowed.

Solution.

Given:

• Sum borrowed at 20% p.a. compound interest.
• Repayment in 3 annual installments at
  the end of each year.
• First installment = Rs. 1200
• Second installment = Rs. 1152
• Third installment = Rs. 2592

Calculation:
First Installment:
-At the end of the first year, the amount to be repaid would have grown by 20%. -So, the amount to be repaid at the end of the first year = Rs. 1200+20% of Rs. 1200 Rs. 1200+0.2 Rs. 1200 – Rs. 1200+ Rs. 240 = Rs. 1440.
Second Installment:
-At the end of the second year, the amount to be repaid would have grown by 20%.
-So, the amount to be repaid at the end of the second year Rs. 1152+20% of Rs. 1152 Rs. 1152+0.2″ Rs. 1152 = Rs. 1152+ Rs. 230.4-Rs. 1382.4.

Third Installment:

-At the end of the third year, the amount to be repaid would have grown by 20%. -So, the amount to be repaid at the end of the third year – Rs. 2592+20% of Rs. 2592 Rs. 2592 +0.2 Rs. 2592 = Rs 2592 + Rs * 0.518 * 0.4 = Rs * 0.311 * 0.4
Now, we can form an equation based on the given information:
P+P+20/100+P20/100+P*20/100 = Rs * 0.144 + Rs * 0.13B * 2.4 + Rs * 0.311 * 0.4
Simplifying the equation:
P + 0.2P + 0.2P + 0.2P = Rs * 0.144 + Rs . 1382.4+ Rs. 3110.4
1.6P = Rs * 0.5932 * 0.8
P = Rs * 0.59328 / 1.6
P = Rs * 0.37O8

Therefore, the sum borrowed is Rs. 3708.
Answer:
Hence, option ‘B’ Rs. 3300 is incorrect. The correct answer is Rs. 3708.

Q.6. The RBI lends a certain amount to the SBI on SI for 2 years at 20%.The SBI gives this entire amount to Bharti Telecom on Cl for 2years at same rate annually. Find the percentage earning of the SBI at the end of 2years on the entire amount?

Solution.

Principal amount (P) = Amount lent by RBI to SBI- Amount given by SBI to Bharti Telecom
Time (t) – 2 years
Rate of interest (R) – 20%
First, let’s calculate the amount received by SBI from RBI after 2 years of Simple Interest (SI).
Using the formula, SI=(PRt)/100 SI(P202)/100 SI = 0.4P
Amount received by SBI (A) – P+ Sl A=P+0.4P
A-1.4P
Now, let’s calculate the amount received by Bharti Telecom from SBI after 2 years of Compound Interest (CI). Using the formula, A-P(1+R/100)^t A=P(1+20/100)^2 A-P(1.2)^2 A = 1.44P

Earning of SBI after 2 years
Interest earned by SBI – Amount
received by Bharti Telecom Amount
received from RBI
Interest earned by SBI-1.44P-1.4P
Interest earned by SBI = 0.04P
Percentage earning of SBI = (Interest earned by SBI/Amount received from RBI) 100
Percentage earning of SBI – (0.04P/ 1.4P)* 100
Percentage earning of SBI = 2.86%
Hence, the SBI earns a percentage of 2.86% on the entire amount after 2 years.

Q.7. A certain sum of money amounts to 31 o Rs. 873 in 32 Rs. 756 in 2 years and to l years at a certain rate of simple interest. What is the rate of interest per annum?

Solution.

Amount in 2 years = Rs. 756
Amount tis 3 years- Rs. 873
Interest for 1-years – Rs. 873- Rs. 756 –
Rs. 117 Interest for 2 years – 117×2-117×2×2
Rs. 156
Interest for 1 year 117×2 – Rs. 78

Principal = Amount Interest…..(for 2
years) Rs. 756-Rs. 156 – Rs. 600
Rate of interest 78×100 600×1 13% р.а.

Q. 8. A person closes his account in an investment scheme by withdrawing Rs. 10000. One year ago, he had withdrawn Rs. 6000. Two years ago he had withdrawn Rs. 5000. Three years ago he had not withdrawn any money. How much money had he deposited approximately at the time of opening the account 4 years ago, if the annual rate of compound interest is 10%

Solution.

Suppose person has deposited Rs. X at the time of opening account.

After one year, he had is. (x + (x10x1)/100) Rs. 11x/10
After two years, he had Rs. ((11x/10)+(11x/10)×(101)/100) = 121x/100
After withdrawing Rs 5000 from Ra. 121x, the balance Rs. (121x-500000)/100
After 3 years, he had (121x-500000)/100+(121x-500000)/100 × (10x 1)/100
(11(121x-500000))/1000

After withdrawing 5000 from above, the balance (1331x/1000)-11500
After 4 years, he had (11/10) ((1331x/1000)-11500)-10000-0 → Rs. 15470

Test your Caliber with us!

Try your knowledge of this idea by solving the questions given on FundaMakers. Click on ‘Question Bank’ to access the ‘CAT question bank’

CAT QUESTION BANK

Visit the link below to learn how to solve Time & Work Questions:

https://fundamakers.com/?p=12653