A number system in mathematics is a writing system for expressing numbers. It is a mathematical notation for representing numbers of a given set, using digits or symbols in a consistent manner. The most common number systems include:
Decimal Number System (Base-10):
- Uses ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
- The position of each digit represents a power of 10.
- Example: 345 in decimal means 3×102+4×101+5×1003×102+4×101+5×100.
Binary Number System (Base-2):
- Uses two digits: 0 and 1.
- Each position represents a power of 2.
- Example: 1011 in binary means 1×23+0×22+1×21+1×201×23+0×22+1×21+1×20, which equals 11 in decimal.
Octal Number System (Base-8):
- Uses eight digits: 0, 1, 2, 3, 4, 5, 6, 7.
- Each position represents a power of 8.
- Example: 157 in octal means 1×82+5×81+7×801×82+5×81+7×80, which equals 111 in decimal.
Hexadecimal Number System (Base-16):
- Uses sixteen symbols: 0-9 and A-F (where A=10, B=11, C=12, D=13, E=14, F=15).
- Each position represents a power of 16.
- Example: 1A3 in hexadecimal means 1×162+10×161+3×1601×162+10×161+3×160, which equals 419 in decimal.
Roman Numerals:
- Uses combinations of letters from the Latin alphabet: I, V, X, L, C, D, M.
- Example: XVII means 10 + 5 + 1 + 1 = 17.
Natural Numbers:
- Positive integers starting from 1, 2, 3, and so on.
- Sometimes 0 is included in this set.
Rational Numbers:
- Numbers that can be expressed as the quotient or fraction 𝑝/𝑞, where 𝑝 and 𝑞 are integers and 𝑞≠0.
Irrational Numbers:
- Numbers that cannot be expressed as a simple fraction.
- Their decimal expansion is non-repeating and non-terminating, e.g., 𝜋, under root 2.
Real Numbers:
- All numbers on the number line, including both rational and irrational numbers.
Complex Numbers:
- Numbers in the form 𝑎+𝑏𝑖, where 𝑎 and 𝑏 are real numbers and 𝑖 is the imaginary unit, with the property that 𝑖2= -1.
Number System Chart
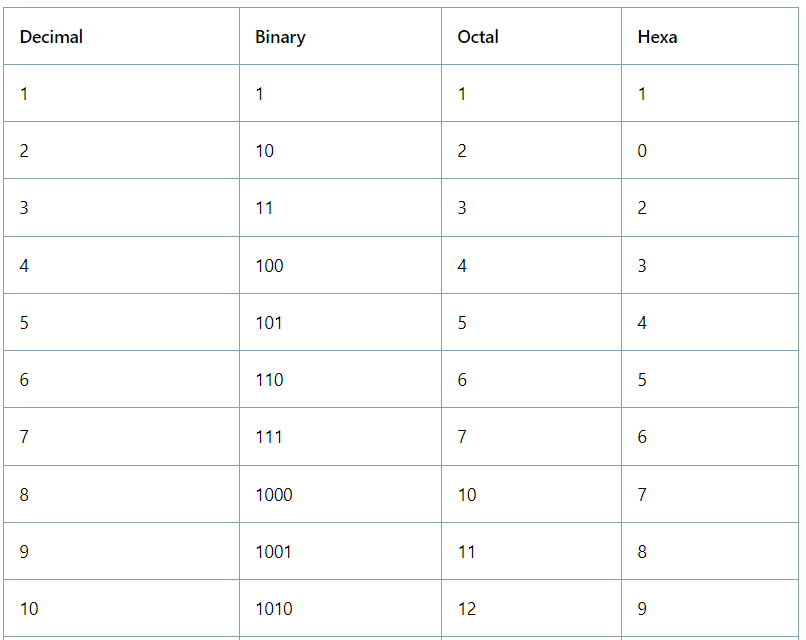
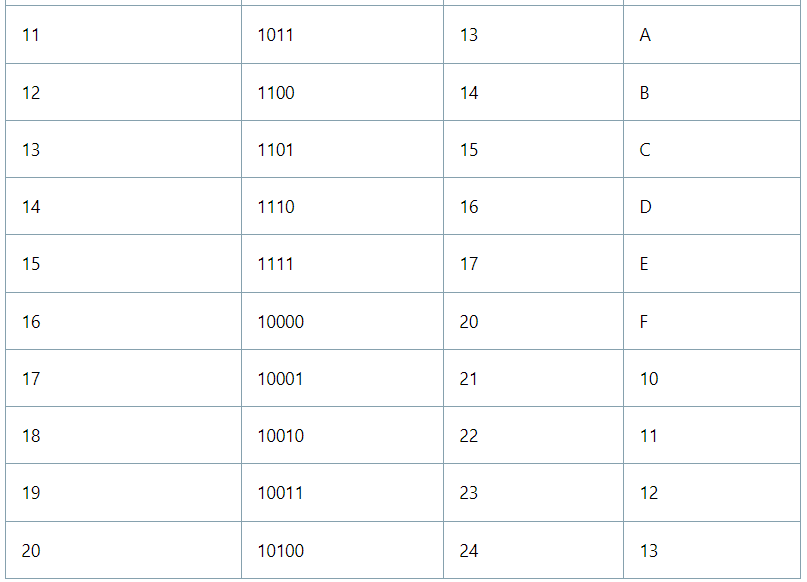
Solved Examples of Questions based on Number System
Q.1. The sum of two numbers is 156 and their HCF is 13. The numbers of such number pair is?
Solution.
Given:
Sum of the numbers = 156
H.C.F of numbers = 13
Concept used:
If the H.C.F of two numbers is H, then the numbers are Hx and Hy. Where x and y are relatively prime numbers or coprimes.
Calculation:
Let numbers are 13x and 13y, where x and y are coprime
Now, 13x + 13y = 156
13 (x + y) = 156
x+y =156/13 = 12
.. possible values if x and y are
(x = 1, y = 11)
(x = 5, y = 7)
Therefore, possible numbers of pairs is 2
Q.2. Find the sum of the factors of 3240.
Solution.
Concept:
a, and b must be prime number
Sum of all factors = (a + a + a² + ….. + a) (b + b² + b² + …… + b)
Solution:
3240 23 x 34 x 51 Sum of factors = (2° +21+22+23) (30+31+32+33+34) (50+51) (1+2+4+8) (1+3+9+27+81) (1+5) 15 x 121 x 6 = 10890
.. required sum is 10890
Q.3. Four bells ring simultaneously at starting and an interval of 6 sec, 12 sec, 15 sec and 20 sec respectively. How many times they ring together in 2 hours?
Solution.
Concept: LCM: It is a number which is a multiple of two or more numbers.
CALCULATION:
LCM of (6, 12, 15, 20) = 60
All 4 bells ring together again after every 60 seconds
Now,
In 2 Hours, they ring together = [(2 x 60 x 60)/60] times + 1 (at the starting) = 121 times
: In 2 hours they ring together for 121 times
Q.4. If a number is in the form of 810 x 97 x 78, find the total number of prime factors of the given number.
Solution.
Concept used: If a number of the form xª * yb * zc and so on, then total prime factors = a + b + c ……
Where x, y, z, … are prime numbers
Calculation:
The number 810 x 97 x 78 can be written as (23) 10 x (37)7 x 78
The number can ve written as 230 x 314 x 78
Total number of prime factors = 30 + 14 + 8
.: The total number of prime factors are 52
Q.5. If the 5-digit number 676xy is divisible by 3, 7 and 11, then what is the value of (3x – 5y)?
Solution.
Given:
676xy is divisible by 3, 7 & 11
Concept:
When 676xy is divisible by 3, 7 &11, it will also be divisible by the LCM of 3, 7 &11.
Dividend = Divisor x Quotient + Remainder
Calculation:
LCM (3, 7, 11) = 231
By taking the largest 5-digit number 67699 and divide it by 231.
67699 = 231 x 293 + 16
67699 67683 + 16
67699-1667683 (completely divisible by 231)
. 67683 = 676xy (where x = 8, y = 3)
(3x-5y) = 3 x 8-5×3
24-15=9
.: The required result = 9
Q.6. How many multiples of both 3 and 4 are there from 1 to 100 in total?
Solution.
Formula used:
n(AUB) = n(A) + n(B) n(A∩B)
Calculation:
On dividing 100 by 3 we get a quotient of 33
The number of multiple of 3, n(A) = 33
On dividing 100 by 4 we get a quotient of 25
The number of multiple of 4, n(B) = 25
LCM of 3 and 4 is 12
On dividing 100 by 12 we get a quotient of 8
The number of multiple of 12, n(AB) = 8
The number which is multiple of 3 or 4 = n(AUB)
Now, n(AUB)=n(A) + n(B) n(A∩B)
33+25-8
⇒50
.. The total number multiple of 3 or 4 is 50
Q.7. Which of the following is a divisor of (4915 – 1)?
Solution.
Given:
(49151)
Concept used:
an bn is divisible by (a + b) when n is an even positive integer.
Here, a & b should be prime number.
Calculation:
(4915-1)
=((72)15-1)
=(730-1)
Here, 30 is a positive integer.
According to the concept, (7301) is divisible by (7 + 1) i.e., 8. .. 8 is a divisor of (49151).
Q.8. Insert 3 rational numbers between 4 & 5.
a) 9/25 (b) 37/78
Solution:
In 9/25, the prime factors of denominator are 25 are 5,5,. Thus, it is a terminating decimal.
In 37/78, the prime factors of denominator are 2,3 and 13. Thus, it is a non-terminating decimal.
Q.9. Find 4 rational numbers between 1 & 2.
Solution.
To find 4 rational numbers between 1 and 2, we need to divide and multiply both the numbers by (4 + 1) which is 5. So we get,
1* 5/5= 5/5 and 2* 5/5= 10/5
Therefore the rational numbers are:
5/5, 6/5, 7/5, 8/5, 9/5, 10/5.
Test your Caliber with us!
Try your knowledge of this idea by solving the questions given on FundaMakers. Click on ‘CAT Question Bank’ to access the CAT question bank.
Visit the link below to learn how to solve questions based on Mensuration with the help of given formulas and solved examples:
https://fundamakers.com/?p=12730





