Mixture and Alligation- Concept
A mixture, as the name implies, is the combination of two or more items, and alligation allows us to determine the ratio in which the ingredients/objects were combined and at what price they are solely profitable or losing money.
To tackle mixture and alligation issues, one must first understand that alligation is used to calculate the mean value of a mixture when the ratio and amount of materials blended change, as well as to determine the proportion in which the elements are mixed.
Alligation Rule: Alligation problems involve the application of the weighted average concept of average. You must be already aware that if we have 1, 2, 3, ………………, k sets, each containing n1, n2, n3, …………… nx elements, and the average of set k is represented by Ak then the weighted average of all the sets together is calculated as
Aw = n1 A1 +n2 A2 + ………. + nk Ak / n1 + n2 + ………..nk
In general, many inquiries specify that two different-priced items are combined to create a mixture. In certain instances, the following formula is used:
Quantity of cheaper ingredient / Quantity of dearer ingredient = Cost of dearer ingredient – Mean Price / Mean Price – Cost price of a cheaper ingredient
The price per unit of the final mixture is called the mean price or weighted price.
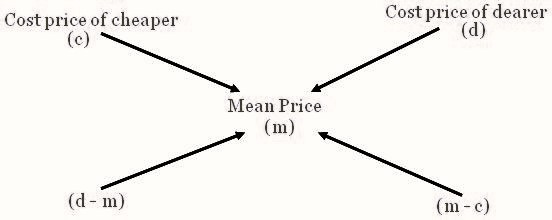
Mixture & Alligation Formula
The basic formula for calculating the ratio in which the materials are blended is:
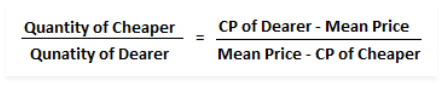
Solved Examples
Mixture & Alligations
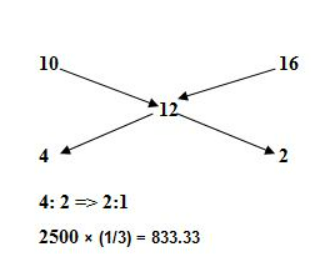
Q. A merchant has 2500 kg of rice, part of which he sells at 10% profit and the rest at 16% Profit He gains 12% overall. The quantity sold at 16% profit?
Solution.
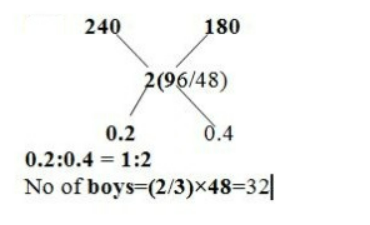
Q. Sum of Rs.96 was shared among 48 boys and girls, receive each girl receive Rs.2.40 and boy Rs.1.80. How much amount did boys get?
Solution.
Q. The milk and water in two vessels A and B are in the ratio 4:3 and 2:3 respectively. In what ratio the liquids in both the vessels be mixed to obtain a new mixture in vessel c consisting half milk and half water?
Solution.
Given:
In-vessel A the quantity of milk = (4/7)X
In-vessel B the quantity of milk = (2/5)Y
Concept Used:
Initial Quantity = Final Quantity
Calculation:
According to question
(4/7)X + (2/5)Y = (1/2) x (X + Y)
X: Y = 7:5
.. The required ratio taken from Vessel A & B is 14: 10 or 7:5
Q. Milk contains 15% water. What quantity of pure milk should be added to 50 litres of milk to reduce the quantity of water to 12%?
Solution.
=50*5/100
=(50+x)*12/100
=7.5*100= 600+12x
=12x = 150 X
= 150/12= 12.5litre
Q. An alloy of gold, silver and bronze contains 90% bronze, 7% gold and 3% silver. A second alloy of bronze and silver only is melted with the first and the mixture contains 85% of bronze, 5% of gold and 10% of silver. Find the percentage of bronze in the second alloy.
Solution.
Since we are working for %, we can assume some value for the initial alloy..
So let’s take it 100 and B:G:S is 90:7:3
Now another alloy, A, is added to it and gold becomes 5% BUT the gold is not added at all..
So 7% of initial total becomes 5% of the new total 5% of new total = 7
So, new total = 7 * 100 140
Thus new alloy, A, added 140-100=40
Now let’s concentrate on the bronze..
Bronze is 85% of new total = 140*85/100= 119
So increase in bronze=119-90-29=quantity of bronze in new alloy,A.
So % of bronze in A=100 * 29/40 = 72.5%
Removal and Replacement
Q. A vessel contains 63 litres of a mixture of milk and water. The ratio of milk to water is 3:4. If 14 litres of mixture is taken out from that vessel and then 6 lItres of water added to it. What will be the percentage of milk in the final mixture?
Solution.
Milk: 63 x (3/7) = 27lit
Water: 63 x (4/7) =36lit
Milk in 14 lit mixture = 14 x (3/7) = 6lit
New mixture (6314+6) = 55 lit
Milk in new mix 27-621
% of milk in the mix = (21/55) x 100 = 38.18% = 38%
Mixed
Q. Two vessels P and Q, contains a mixture of milk and water in the ratio of 6 : 2 and 5: 11 respectively. When the equal quantities of these two vessels are taken into a third vessel R, then what is the ratio of milk and water in R?
Solution.
Given that,
Let the quantity of milk and water be denoted as x and y
P Milk= 6x/8; P Water= 2y/8
Q milk= 5x/6; Water= 11y/16
According to the question
Equal quantity from both the vessel has been taken
Download Solution PDF
milk/water = (6x/8 + 5x/16)/(2y/8 + 11y/16) = (17x/16)/(15y/16) = 17/15
Required ratio of milk and water is 17:15
Q. Arun has 13 boxes of chocolates with him, with an average of 17 chocolates per box. If each box has at least 11 chocolates and no two boxes have equal number of chocolates, then what can be the maximum possible number of chocolates in any box?
Solution.
Total number of chocolates = 13 17 = 221
For one box to have maximum number of chocolates,
the other boxes need to have minimum number of chocolates i.e. 11, 12, 22
Total 11*12+ (0+1+2+…+11)
132 +66 198
Therefore, maximum possible chocolates = 221-198 = 23
Test your Caliber with us!
Try your knowledge of this idea by solving the questions given on FundaMakers. Click on ‘CAT Question Bank’ to access the CAT question bank.
Visit the link below to learn how to solve problems based on Number System:





