Percentage
A value or ratio that may be stated as a fraction of 100 is called a percentage in mathematics. Divide the number by the whole and multiply the result by 100 if we need to get the percentage of a given number. As a result, the percentage denotes a fraction per hundred. The definition of percent is per 100. “%” is the symbol used to represent it.
Percentage Formula:
To determine the percentage, we have to divide the value by the total value and then multiply the resultant by 100.
Percentage formula = (Value/Total value) × 100
Example: 6/4 × 100 = 1.5 × 100 = 150 per cent
How to Calculate Percentage?
We must use a separate formula, such as this one, to determine the percentage of a number.
P/% of Total = X
where X is the necessary proportion.
In order to represent the aforementioned formulas, we must eliminate the % symbol.
P/100 * Number = X
Example: Calculate 10% of 60
Let 10% of 60 = x
10/100*60= x
x = 6
Converting Fractions into Percentage:
A fraction can be represented by a/b, Multiplying and Dividing the fraction by 100, we have
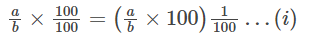
From the definition of percentage, we have;
(1/100) = 1%
Thus, equation (i) can be written as:
(a/b) × 100%
Therefore, a fraction can be converted to a percentage simply by multiplying the given fraction by 100.
Conversion of Fraction into Percentage
Percentage Difference Formula :
The following formula can be used to determine the percentage difference between two values if we are given two values:

Percentage Increase and Decrease:
The original number is subtracted from a new number, divided by the original number, and then multiplied by 100 to get the percentage increase.
% increase = [(New number – Original number)/Original number] x 100
where, increase in number = New number – original number
Comparably, a percentage drop is calculated by deducting a new figure from the base number, dividing the result by the base number, and then multiplying the result by 100.
% decrease = [(Original number – New number)/Original number] x 100
Where decrease in number = Original number – New number
So basically if the answer is negative then there is a percentage decrease.
Percentage Questions
Q.1. If 12% of 50% of a number is 12, then find the number?
Solution:
Let the required number be x,
Therefore, as per the given question
(12/100) * (50/100)* x = 12
So, x= ( 10*100*100)/(12*50) = 200
Q.2. What percentage of 1/5 is 1/35 ?
Solution:
let x% of 1/5 is 1/25
Therefore, [(1/5)/100] * x = 1/25
x= 1/25* 5/1 * 100= 4%
Q.3. Which number is 60% less than 80?
Solution:
Required number= 40% of 80
(80*40)/100 = 32
Therefore, the number 32 is 60%, less than 80.
Q.4. The sum of (10% OF 12.5) and (6% of 25.2) is equal to what value?
Solution:
As per the given question,
Sum= (10% of 12.5) + (6% of 25.2)
(12.55*10)/10 + (6* 25.2)/100
= 14.012
Word Problem
Q.1 A lady spends her total income as follows-30% on food, 25% on rent, 16% on travel and 19% on education. After all expenses made, she saves Rs. 8,900. Find the amount spent on education.
Solution:
Given, A lady spends 30% of her income on food, 25% on rent, 16% on travel and 19% on education.
Her total saving: 8,900
Concepts used: Expenditure + Saving+ Income
Calculation:
Let the income earned by lady be Rs. x
Expenditure made by lady on food= 30% of x = 0.30x
Expenditure made by lady on rent= 25% of x= 0.25x
Expenditure made by lady on travel= 16% of x= 0.16x
Expenditure made by man on education = 19% of x = 0.19x
Savings= Rs. 8,900
Income= Expenditure + Savings
x=0.30x+0.25x+0.16x+0.19x+Rs.8,900
x=0.90x+ Rs.8,900
x-0.90x=Rs.8,900
0.10x= Rs.8,900/0.10
x=Rs.89,000
Expenditure made by lady on education= 19% of x
0.19*Rs.89,000= Rs.16,910
Thus, the expenditure made on education by the lady is equal to Rs.16,910
Q.2. On a shelf, the first row contains 15% more books than the second row and the third row contains 15% less books than the second row. If the total number of books contained in all the rows is 900, then find the number of books in the first row.
Solution:
Let the number of books on second row be 100x
Then, 1st row=
Given, the books on first row contains 15% more books than the second row
Thus, 1st row= 100x+15x= 115x
2nd row= 100x
3rd row=
Given, the books on second row contains 15% less books than second row
Thus, 3rd row= 100x-15x= 85x
Total number of books= 115x+100x+85x= 300x
According to the question, 300x=900
x= 3
So, on 1st row = 115*3= 345 books.
Q.3. A television depreciates in value each year at the rate of 10% of its previous value. However, every second year there is some maintenance work so that in that particular year, depreciation is only 5% of its previous value. If at the end of the fourth year , the value of the television stands at Rs. 1,46,205, then the value of the television at the start of the first year.
Solution:
Let the value of television at the start of first year be Rs. x
According to the question, x*90/100*95/100*90/100*95/100= 1,46,205
x= 1,46,205*10,00,000/81*95*95
x= Rs. 2,00,000
Q.4. In a mixture of 80 litres of mineral oil and edible oil, 25% of the mixture is mineral oil. How much edible oil should be added to the mixture so that mineral oil becomes 20% of the mixture?
Solution:
In a mixture of 80 litres of mineral and edible oil, 25% of the mixture is mineral oil.
Calculation:
Amount of Mineral oil= 80*25/100= 20 litres
Let x be the amount of edible oil added
ATQ,, 20=20% of (80+x)
20= 20/100 (80+x)
100=80+x
x+20 litres= x= 20 lts
Q.5. There are three solutions, A, B and C containing milk and water. The strength of the three solutions are 80%,90%, and 70% respectively. When 1 litre each of A and B is mixed with C, the strength of C increases to 75%. What would be strength of C if two litres of A and 0.5 litres of B were mixed with C?
Solution:
Let the volume of C be x litres.
As the strengths of A and B are 80% and 90%, by mixing 1 litre each of A and B with C, we are adding 300 ml and 900 ml respectively of alcohol to C. The strenth of C is 70% which increases to 75%.
So, the new strength = 75%
7x/10+ 1.7/x+2 = 75/100
On solving we get x= 4 litres
So, alcohol present in C= 70% of 4 litres= 2.8 litres
In the second case, total alcohol added= (1.6+0.45) ltrs= 2.05 ltrs
Required strength = 2.8+2.05/4=2.5 = 74.6%
Test your Caliber with us!
Try your knowledge of this idea by solving the questions given on FundaMakers. Click on ‘Question Bank’ to access the question bank.
Visit the link below to learn how to solve problems based on Profit & Loss:




